Lindenmayer, Koch und die berechnete Natur
 Die dunklen Tage läuten den Winter ein. Und was fehlt uns hierzulande dann so oft? Na klar, Schnee! Da ist es doch schön, wenn man was studiert hat, bei dem sich vielleicht doch noch eine Lösung finden lässt. Schneeflocken kann man sich nämlich auch per Programm erzeugen.
Die dunklen Tage läuten den Winter ein. Und was fehlt uns hierzulande dann so oft? Na klar, Schnee! Da ist es doch schön, wenn man was studiert hat, bei dem sich vielleicht doch noch eine Lösung finden lässt. Schneeflocken kann man sich nämlich auch per Programm erzeugen.
Das ist gar nicht mal so schwer. Mit einem sehr simplen Algorithmus kann aus einem einfachen Dreieck eine sehr hübsche Flocke entstehen. Ein paar Ergänzungen, und es werden auch viele verschiedene Flocken: mathworld.wolfram.com/KochSnowflake.html.
 Das Basisrezept
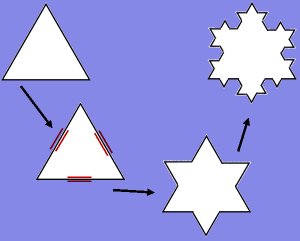
Das Basisrezept
Man nehme ein gleichseitiges Dreieck.
Jede gerade Linie (also jede Seite des Dreiecks) ersetze man nun wie folgt:
Die Linie dritteln, das mittlere Drittel herausnehmen und durch zwei genauso lange Stücke ersetzen, die einen spitzen Winkel auf der ursprünglichen Linie bilden.
Je öfter man das tut, desto weicher wird die Schneeflocke.
Erstaunlich
Die Koch’sche Schneeflocke ist nicht nur hübsch anzusehen, sondern hat auch erstaunliche Eigenschaften. Sie ist unendlich lang, passt aber trotzdem immer in dasselbe Quadrat, das man als äußere Begrenzung um das erste Ergebnis aus dem Ursprungsdreieck ziehen kann. 
Und: Unter einer Lupe betrachtet, ist jeder Abschnitt der Außenlinie einem anderen Abschnitt ähnlich, der nicht vergrößert ist.
Den mathematischen Hintergrund dazu kann man auf einer englischen Matheseite nachlesen: scidiv.bellevuecollege.edu/MATH/Snowflake.html.
Lindenmayer-Systeme
Die Kochkurve gehört zum selben Informatikfeld wie die Lindenmayer-Systeme. Diese Systeme erzeugen durch Algorithmen komplexe Formen. Da lassen sich sogar Sträucher „pflanzen“, die der Wirklichkeit verblüffend ähnlich sind: www.inkscape.org/screenshots/gallery/inkscape-0.44-lindenmayer.png.
Wer mehr über L-Systeme erfahren will, findet an der Uni Mainz eine gute Zusammenfassung: www.informatik.uni-mainz.de/lehre/cg/SS2006_SCG/talks/LindenmayerSystems/LindenmayerSysteme.pdf
 Ein wunderschönes Buch gibt es auch: „The Algorithmic Beauty of Plants“ als PDF-Download oder als Papierversion (Antiquariat).
Ein wunderschönes Buch gibt es auch: „The Algorithmic Beauty of Plants“ als PDF-Download oder als Papierversion (Antiquariat).